The bound states of the hydrogen atom are governed by the geometrical symmetry 
(not considering the full dynamical symmetry 
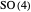). Similarly, the two-dimensional isotropic harmonic oscillator exhibits the symmetry 
.
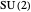To anyone versed in the theory of Lie groups, it would not be
surprising that there might be an explicit connection between these two
problems, in view of the local isomorphism between the corresponding Lie
algebras 
and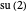 
.
Contributed by: S. M. Blinder (March 2019)
Open content licensed under CC BY-NC-SA
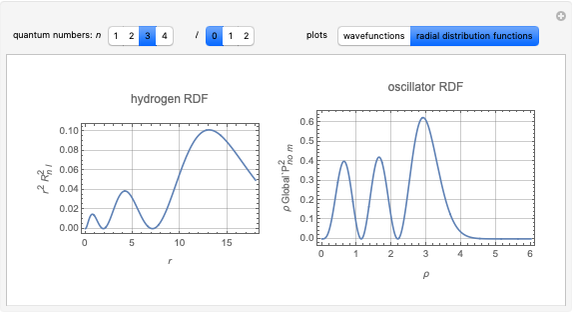
Snapshots
Details
Julian
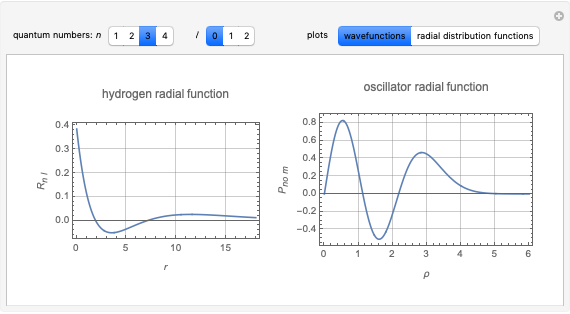
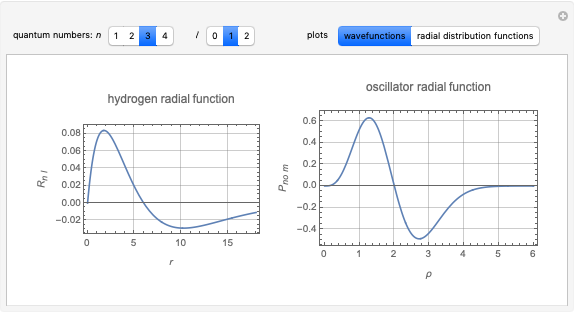
Schwinger, in his quantum mechanics course [1], suggested a very clever
method to solve the hydrogen-atom problem by converting it into the
equation for a two-dimensional isotropic harmonic oscillator. To do
this, let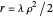 
and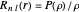 
. Then 
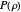turns out to obey the radial equation for the oscillator.
The method is given as a problem in [1].
Reference
[1] G. Baym, Lectures on Quantum Mechanics, New York: W. A. Benjamin, 1969 p. 179.
Permanent Citation
https://demonstrations.wolfram.com/ConnectionBetweenQuantumMechanicalHydrogenAtomAndHarmonicOsc/
No comments:
Post a Comment