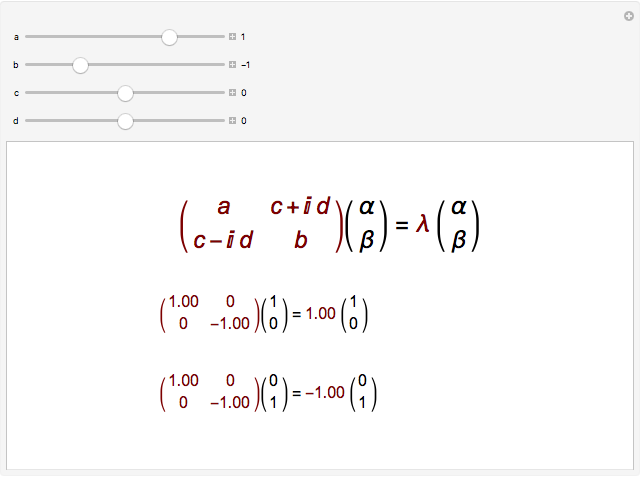
Eigenvalue Problem for 2×2 Hermitian Matrices
b |
c |
d |

An  Hermitian matrix (
Hermitian matrix (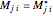 ) has
) has  real eigenvalues and
real eigenvalues and  mutually orthogonal eigenvectors, which can be chosen to be normalized. This Demonstration considers the case of
mutually orthogonal eigenvectors, which can be chosen to be normalized. This Demonstration considers the case of 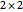 Hermitian matrices, which has important applications in the study of two-level quantum systems. For a selected
Hermitian matrices, which has important applications in the study of two-level quantum systems. For a selected 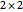 Hermitian matrix, the graphic shows the equations satisfied by the two
eigenvalues, with their corresponding orthonormalized eigenvectors.
Hermitian matrix, the graphic shows the equations satisfied by the two
eigenvalues, with their corresponding orthonormalized eigenvectors.
Contributed by: S. M. Blinder (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Snapshots 1-3: eigenvalue equations for the three Pauli spin matrices 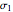 ,
,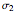 ,
, 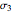
Permanent Citation
https://demonstrations.wolfram.com/EigenvalueProblemFor22HermitianMatrices/







No comments:
Post a Comment