γ |
3 2 | |
α | |
γ |
1 2 | |
α | |
β |
3 2 | |
α | |
β |
|

The ground state of the helium atom has the electronic configuration  S. In the lowest excited states, an electron is promoted from the
S. In the lowest excited states, an electron is promoted from the  to a
to a  or
or  orbital. Although the hydrogenic
orbital. Although the hydrogenic  and
and  orbitals are degenerate, the
orbitals are degenerate, the  configuration of helium has a lower energy than the
configuration of helium has a lower energy than the  . This is attributed to the greater shielding of the nuclear charge experienced by the
. This is attributed to the greater shielding of the nuclear charge experienced by the  orbital. Each of these lowest excited configurations is further split
into a singlet and a triplet state, depending on whether the electron
spins are antiparallel or parallel. (They must be antiparallel in the
1sInlineMathItalic2 configuration, by virtue of the Pauli exclusion
principle, so that the ground state is a singlet.) The energies of the
four lowest excited states can be calculated to fairly reasonable
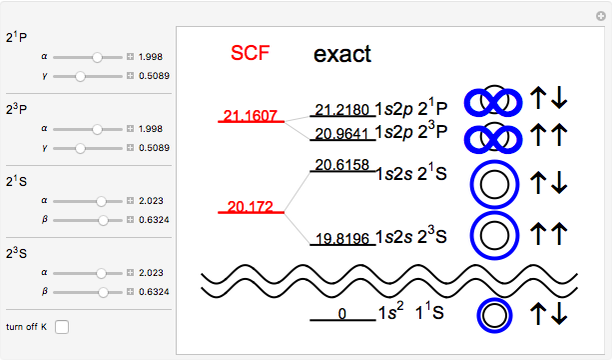
accuracy by self-consistent field (SCF) theory. In this Demonstration,
the orbitals are approximated by the simple forms:
orbital. Each of these lowest excited configurations is further split
into a singlet and a triplet state, depending on whether the electron
spins are antiparallel or parallel. (They must be antiparallel in the
1sInlineMathItalic2 configuration, by virtue of the Pauli exclusion
principle, so that the ground state is a singlet.) The energies of the
four lowest excited states can be calculated to fairly reasonable
accuracy by self-consistent field (SCF) theory. In this Demonstration,
the orbitals are approximated by the simple forms:  ,
,  and
and  . According to the Hartree-Fock method, the energy of a two-electron state is given by
. According to the Hartree-Fock method, the energy of a two-electron state is given by  . The one-electron integrals
. The one-electron integrals  account for the kinetic energy and nuclear attraction. Atomic units are used, with
account for the kinetic energy and nuclear attraction. Atomic units are used, with  . The Coulomb integrals
. The Coulomb integrals  represent the electrostatic repulsion between the two orbital charge distributions. The exchange integrals
represent the electrostatic repulsion between the two orbital charge distributions. The exchange integrals  have no classical analog. They are a consequence of the
quantum-mechanical exchange symmetry of the atomic wavefunction. The +
and
have no classical analog. They are a consequence of the
quantum-mechanical exchange symmetry of the atomic wavefunction. The +
and  signs in the energy expression pertain to the singlet and triplet
states, respectively. The SCF energy can be optimized by variation of
the parameters
signs in the energy expression pertain to the singlet and triplet
states, respectively. The SCF energy can be optimized by variation of
the parameters  ,
,  ,
,  ,
which you can do in the Demonstration. All energies are expressed in
electron volts above the ground state. See how closely you can
approximate the exact
,
which you can do in the Demonstration. All energies are expressed in
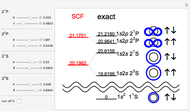
electron volts above the ground state. See how closely you can
approximate the exact  S,
S,  S,
S,  P and
P and  P energies, which are represented by black dashes. The
P energies, which are represented by black dashes. The  S,
S,  P and
P and  P
states are the lowest of their symmetry type, thus the calculated
energies are upper bounds to the corresponding exact values, by virtue
of the variational principle. This is not true for the
P
states are the lowest of their symmetry type, thus the calculated
energies are upper bounds to the corresponding exact values, by virtue
of the variational principle. This is not true for the  S
computation, however, since there exists a lower state of the same
symmetry; it is just an approximation which can be higher or lower than
the exact value.
S
computation, however, since there exists a lower state of the same
symmetry; it is just an approximation which can be higher or lower than
the exact value.
Contributed by: S. M. Blinder (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Snapshot 1: optimized values of  ,
,  ,
,  in a Hartree-Fock computation
in a Hartree-Fock computation
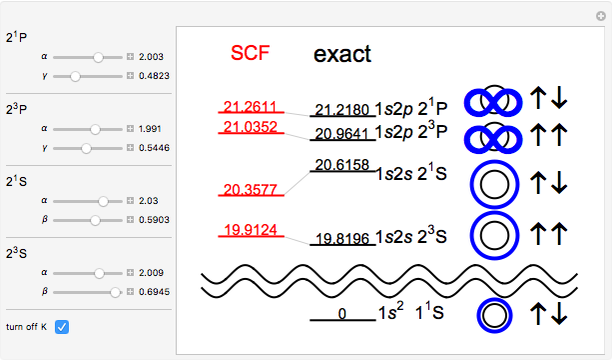
Snapshot 2: setting the exchange integrals equal to zero collapses the singlet and triplet states of each configuration
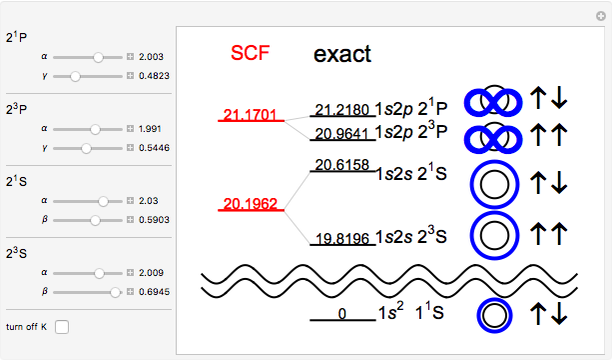
Snapshot 3: optimized results using Hartree's original SCF method, without exchange
References: S. M. Blinder, Introduction to Quantum Mechanics, Amsterdam: Elsevier, 2004, pp. 119-121
H. A. Bethe and E. E. Salpeter, Quantum Mechanics of One- and Two-Electron Atoms, New York: Academic Press, 1957, pp. 157-160.
Permanent Citation
https://demonstrations.wolfram.com/LowerExcitedStatesOfHeliumAtom/


No comments:
Post a Comment