Slater's rules for effective nuclear charge

1. Slater's Rules, the steps

Slater Type Orbitals (STO) are an approximation and do not represent the realistic orbitals. This oversimplified model is found according to the semi-empirical results.

In the STO, the nuclear charge Z and the principal quantum number n are replaced by the effective nuclear charge Z^*, and the effective principal quantum number n^* respectively; in order to fit the two following formula for the radial function and energy of any electron in any atom:

R(r) = N_r r^{n* - 1} exp {- (Z^*/n^*) r}
N_r is the normalization constant for different orbitals.
E = - (Z^*/n^*)² (13.6 eV)

---

R(r) = N_r r^n*-1 exp {- (Z^*/n^*) r}
N_r is the normalization constant for different orbitals
E = - (Z^*/n^*)² (13.6 eV)

---

Here are the Slater's rules to calculate an approximate value for the effective nuclear charge "felt" by an electron in a particular orbital of an atom.

1 - Write the electronic configuration for the atom using the following grouping, called Slater electron configuration:

(1s) (2s,2p) (3s,3p) (3d) (4s,4p) (4d) (4f) (5s,5p) ... ,

2 - Any electron to the right of the considered electron of interest do not contribute to shielding,

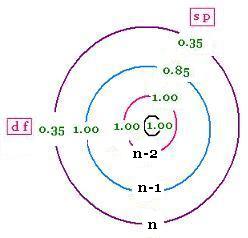
3 - All other electrons in the same group of the considered electron shield by 0.35 nuclear charge units each; except for 1s, the screening is reduced to 0.30,

4 - If the considered electron is an s or p electron in the shell of principal quantum number n, all electrons with one less value n-1 shield by 0.85 units of nuclear charge each; and all electrons with two less values n-2 shield by 1.00 units. The n-3, n-4, ... shield by 1.00 units each as well.

5 - If the considered electron is an d or f electron: all electrons to the left shield by 1.00 units of nuclear charge each.

6 - Sum all the shielding amounts for each group. To obtain the effective charge for each group, subtract from the nuclear charge value the corresponding shielding.

7 - For larger principal quantum numbers, n is corrected as follows:
n = 1, 2, 3, 4, 5, 6
n^* = 1, 2, 3, 3.7, 4.0, 4.2 

2. Example:

Ruthenium atom: Ru: Z = 44

(1s2) (2s2 2p6) (3s2 3p6) (3d10) (4s2 4p6) (4d7) (5s1)

S(1s2) = 1 * 0.35 = 0.35
S(2s2 2p6) = 7 * 0.35 + 2 * 0.85 = 4.15
S(3s2 3p6) = 7 * 0.35 + 8 * 0.85 + 2 * 1.00 = 11.25
S(3d10) = 9 * 0.35 + 8 * 1.00 + 8 * 1.00 + 2 * 1.00 = 21.15
S(4s2 4p6) = 7 * 0.35 + 18 * 0.85 + 8 * 1.00 + 2 * 1.00 = 27.75
S(4d7) = 6 * 0.35 + 8 * 1.00 + 18 * 1.00 + 8 * 1.0 + 2 * 1.00 = 38.1
S(5s1) = 15 * 0.85 + 18 * 1.00 + 8 * 1.00 + 2 * 1.00 = 40.75


Z_eff(electronic state) = Z - S(electronic state)

Z_eff(1s2) = 44 - 0.35 = 43.7
Z_eff(2s2 2p6) = 44 - 4.15 = 39.85
Z_eff(3s2 3p6) = 44 - 11.25 = 32.75
Z_eff(3d10) = 44 - 21.15 = 22.85
Z_eff(4s2 4p6) = 44 - 27.75 = 16.25
Z_eff(4d7) = 44 - 38.1 = 5.9
Z_eff(5s1) = 44 - 40.75 = 3.25


E (4s2 4p6) = - (16.25/3.7)² (13.6 eV) = - 262.33 eV

3. Z effective calculator:

Enter an atom's symbol
Get its effective nuclear charge

Results:

Iron atom: Nuclear charge: Z = 26 Electronic configuration: [Ar]3d6 4s2  1s2 2s2 2p6 3s2 3p6 3d6 4s2 Slater group: (1s)2 (2s 2p)8 (3s 3p)8 (3d)6 (4s)2 Shielding constant: S (1s2) = 0.3 S (2s2 2p6) = 4.15 S (3s2 3p6) = 11.25 S (3d6) = 19.75 S (4s2) = 22.25  Effective nuclear charge: Zeff (1s2) = 25.7  Zeff (2s2 2p6) = 21.85  Zeff (3s2 3p6) = 14.75  Zeff (3d6) = 6.25  Zeff (4s2) = 3.75

Reference: https://scientificsentence.net/Equations/Quantum/index.php?key=yes&Integer=slater