Monday, September 13, 2021

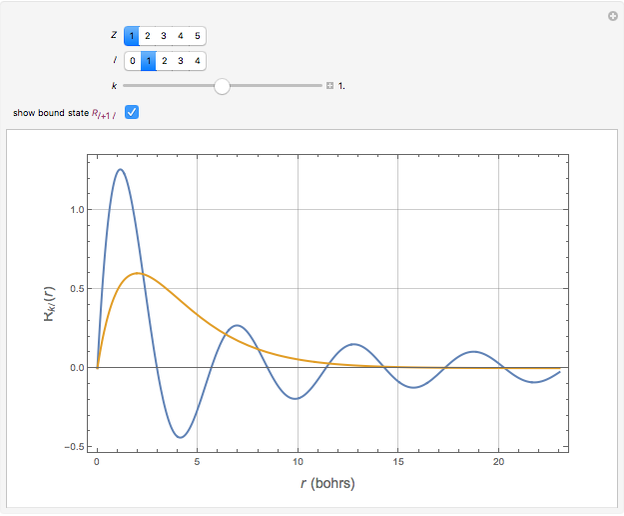
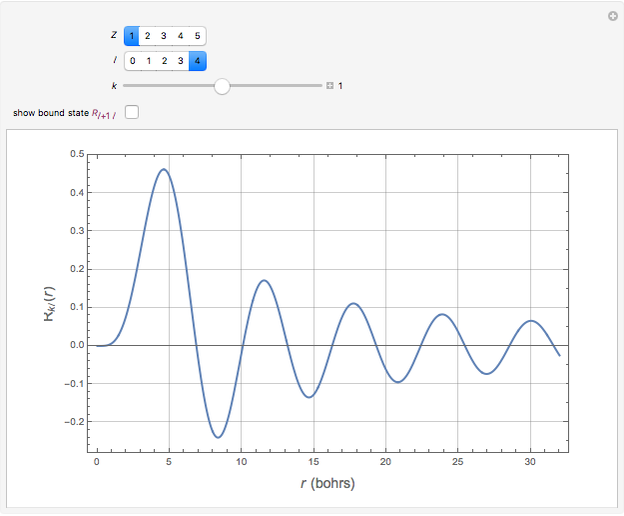
Hydrogen-Like Continuum Eigenstates

Abderrahmane REGGAD 1:09 PM Hydrogen Atom

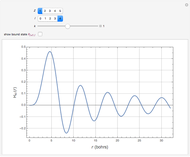
The positive-energy continuum states of a hydrogen-like system are described by the eigenfunctions with corresponding eigenvalues , (). are the same spherical harmonics that occur for the bound states. In atomic units , the radial equation can be written . The solutions with the appropriate analytic and boundary conditions have the form . These functions are deltafunction-normalized, such that . They have the same functional forms (apart from normalization constants) as the discrete eigenfunctions under the substitution .