Relativistic Energy Levels for Hydrogen Atom
| |||

In nonrelativistic quantum mechanics, the energy levels of the hydrogen atom are given by the formula of Bohr and Schrödinger,  ,
expressed in hartrees (assuming the appropriate correction for the
reduced mass of the electron). The energy depends only on the principal
quantum number
,
expressed in hartrees (assuming the appropriate correction for the
reduced mass of the electron). The energy depends only on the principal
quantum number  and is
and is  -fold
degenerate (including electron spin). In Dirac's relativistic theory,
this degeneracy is partially resolved and the energy is found to depend
as well on the angular-momentum quantum number
-fold
degenerate (including electron spin). In Dirac's relativistic theory,
this degeneracy is partially resolved and the energy is found to depend
as well on the angular-momentum quantum number  . To second order in the fine-structure constant
. To second order in the fine-structure constant  , the hydrogen energy levels are given by
, the hydrogen energy levels are given by  . In Dirac's theory, levels such as
. In Dirac's theory, levels such as  and
and  remain degenerate. The discovery of the Lamb shift showed that these
two levels were actually split by 1057.8 MHz. This was a major stimulus
for the development of quantum electrodynamics in the 1950s. The Lamb
shift, significant only for
remain degenerate. The discovery of the Lamb shift showed that these
two levels were actually split by 1057.8 MHz. This was a major stimulus
for the development of quantum electrodynamics in the 1950s. The Lamb
shift, significant only for  -states), raises the energy by approximately
-states), raises the energy by approximately  . The relativistic and radiative correction to hydrogen energy levels can therefore be written
. The relativistic and radiative correction to hydrogen energy levels can therefore be written  , to third order in
, to third order in  .
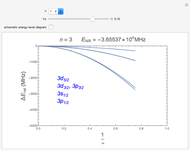
In this Demonstration, you can conceptually vary the fine-structure
constant from 0 to its actual value, or equivalently the speed of light
.
In this Demonstration, you can conceptually vary the fine-structure
constant from 0 to its actual value, or equivalently the speed of light  from
from  to 1 (meaning
to 1 (meaning  m/s), to show the transition from nonrelativistic to relativistic energies for quantum numbers
m/s), to show the transition from nonrelativistic to relativistic energies for quantum numbers  , and
, and  . The energies are expressed in MHz (1 hartree =
. The energies are expressed in MHz (1 hartree =  MHz).
MHz).
Contributed by: S. M. Blinder (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
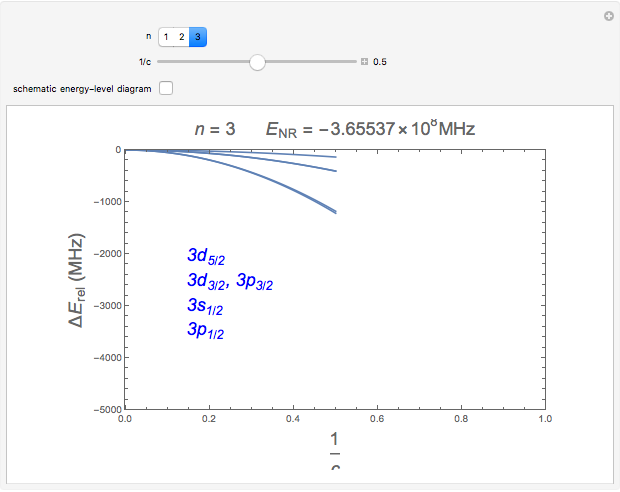
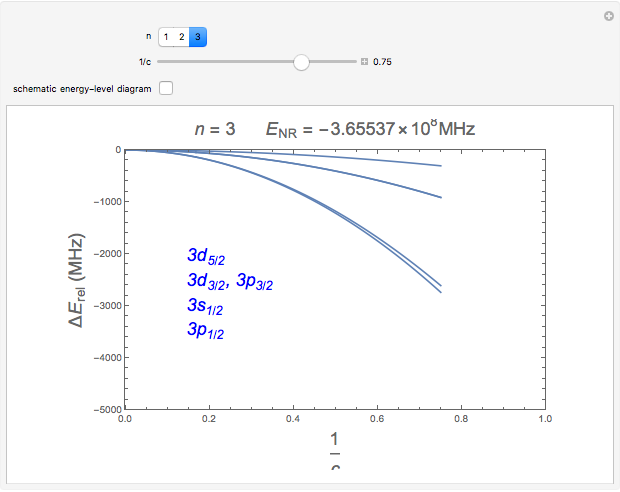
Snapshots 1, 2: relative corrections to  level as speed of light is conceptually decreased from infinity
level as speed of light is conceptually decreased from infinity
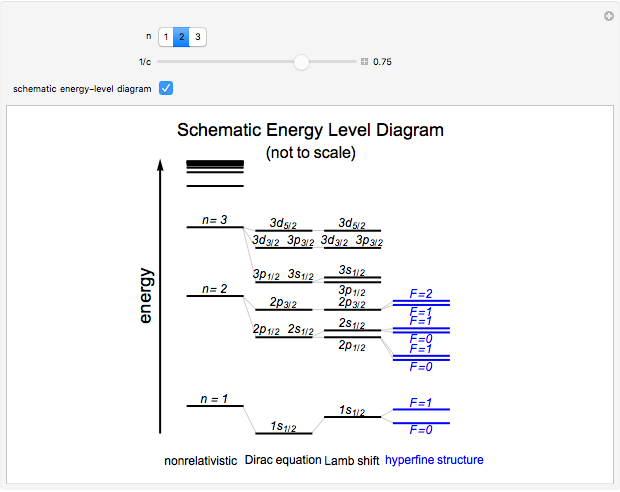
Snapshot 3: schematic hydrogen energy-level diagram for various stages of theory
Permanent Citation
https://demonstrations.wolfram.com/RelativisticEnergyLevelsForHydrogenAtom/



No comments:
Post a Comment